Assignment 3
Assignment 3
1. Rerun murrell01.R and document one of the charts
# Load required libraries
library(grid)
### Paul Murrell's R examples (selected)
## Start plotting from basics
# Note the order
plot(pressure, pch=16) # Scatter plot for Pressure vs Temperature
text(150, 600,
"Pressure (mm Hg)\nversus\nTemperature (Celsius)")
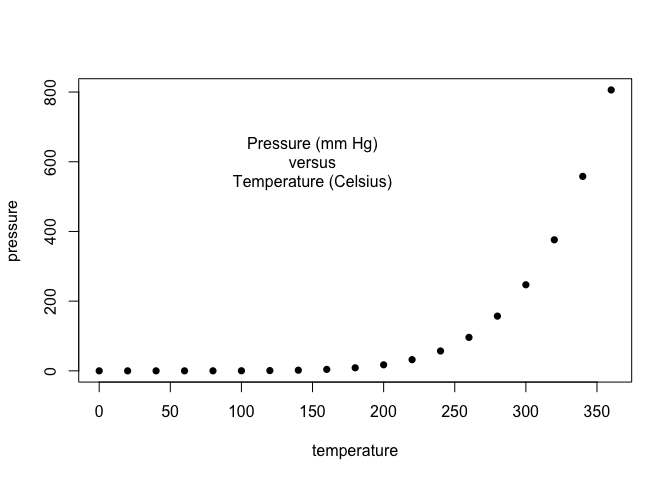
# Documentation:
# The plot function is used to create a scatter plot of the pressure dataset,
# where 'pch' specifies the plotting character. Here, 'pch=16' represents filled circles.
# The text function adds a label to the plot at specified coordinates (150, 600).
2. Rerun anscombe01.R
- Compare the regression models
## Data Visualization for Anscombe's Quartet
data(anscombe) # Load Anscombe's data
head(anscombe) # View the data
## x1 x2 x3 x4 y1 y2 y3 y4
## 1 10 10 10 8 8.04 9.14 7.46 6.58
## 2 8 8 8 8 6.95 8.14 6.77 5.76
## 3 13 13 13 8 7.58 8.74 12.74 7.71
## 4 9 9 9 8 8.81 8.77 7.11 8.84
## 5 11 11 11 8 8.33 9.26 7.81 8.47
## 6 14 14 14 8 9.96 8.10 8.84 7.04
summary(anscombe)
## x1 x2 x3 x4 y1
## Min. : 4.0 Min. : 4.0 Min. : 4.0 Min. : 8 Min. : 4.260
## 1st Qu.: 6.5 1st Qu.: 6.5 1st Qu.: 6.5 1st Qu.: 8 1st Qu.: 6.315
## Median : 9.0 Median : 9.0 Median : 9.0 Median : 8 Median : 7.580
## Mean : 9.0 Mean : 9.0 Mean : 9.0 Mean : 9 Mean : 7.501
## 3rd Qu.:11.5 3rd Qu.:11.5 3rd Qu.:11.5 3rd Qu.: 8 3rd Qu.: 8.570
## Max. :14.0 Max. :14.0 Max. :14.0 Max. :19 Max. :10.840
## y2 y3 y4
## Min. :3.100 Min. : 5.39 Min. : 5.250
## 1st Qu.:6.695 1st Qu.: 6.25 1st Qu.: 6.170
## Median :8.140 Median : 7.11 Median : 7.040
## Mean :7.501 Mean : 7.50 Mean : 7.501
## 3rd Qu.:8.950 3rd Qu.: 7.98 3rd Qu.: 8.190
## Max. :9.260 Max. :12.74 Max. :12.500
# Create four model objects
lm1 <- lm(y1 ~ x1, data=anscombe)
lm2 <- lm(y2 ~ x2, data=anscombe)
lm3 <- lm(y3 ~ x3, data=anscombe)
lm4 <- lm(y4 ~ x4, data=anscombe)
# Compare summary statistics of regression models
summary(lm1)
##
## Call:
## lm(formula = y1 ~ x1, data = anscombe)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.92127 -0.45577 -0.04136 0.70941 1.83882
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.0001 1.1247 2.667 0.02573 *
## x1 0.5001 0.1179 4.241 0.00217 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.237 on 9 degrees of freedom
## Multiple R-squared: 0.6665, Adjusted R-squared: 0.6295
## F-statistic: 17.99 on 1 and 9 DF, p-value: 0.00217
summary(lm2)
##
## Call:
## lm(formula = y2 ~ x2, data = anscombe)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.9009 -0.7609 0.1291 0.9491 1.2691
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.001 1.125 2.667 0.02576 *
## x2 0.500 0.118 4.239 0.00218 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.237 on 9 degrees of freedom
## Multiple R-squared: 0.6662, Adjusted R-squared: 0.6292
## F-statistic: 17.97 on 1 and 9 DF, p-value: 0.002179
summary(lm3)
##
## Call:
## lm(formula = y3 ~ x3, data = anscombe)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.1586 -0.6146 -0.2303 0.1540 3.2411
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.0025 1.1245 2.670 0.02562 *
## x3 0.4997 0.1179 4.239 0.00218 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.236 on 9 degrees of freedom
## Multiple R-squared: 0.6663, Adjusted R-squared: 0.6292
## F-statistic: 17.97 on 1 and 9 DF, p-value: 0.002176
summary(lm4)
##
## Call:
## lm(formula = y4 ~ x4, data = anscombe)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.751 -0.831 0.000 0.809 1.839
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.0017 1.1239 2.671 0.02559 *
## x4 0.4999 0.1178 4.243 0.00216 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.236 on 9 degrees of freedom
## Multiple R-squared: 0.6667, Adjusted R-squared: 0.6297
## F-statistic: 18 on 1 and 9 DF, p-value: 0.002165
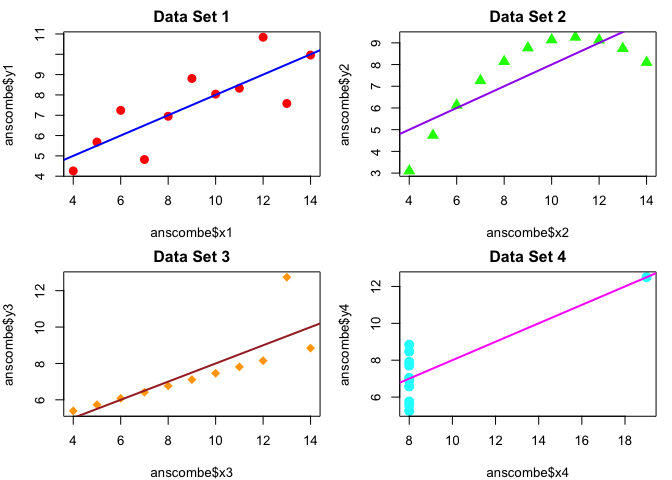
- Compare different ways to create the plots
# Preparing for the plots
par(mfrow = c(2, 2), mar = c(4, 4, 2, 1))
# Plot each dataset with different colors and point characters
plot(anscombe$x1, anscombe$y1, col = "red", pch = 16, cex = 1.5,
main = "Data Set 1")
abline(lm1, col = "blue", lwd = 2)
plot(anscombe$x2, anscombe$y2, col = "green", pch = 17, cex = 1.5,
main = "Data Set 2")
abline(lm2, col = "purple", lwd = 2)
plot(anscombe$x3, anscombe$y3, col = "orange", pch = 18, cex = 1.5,
main = "Data Set 3")
abline(lm3, col = "brown", lwd = 2)
plot(anscombe$x4, anscombe$y4, col = "cyan", pch = 19, cex = 1.5,
main = "Data Set 4")
abline(lm4, col = "magenta", lwd = 2)
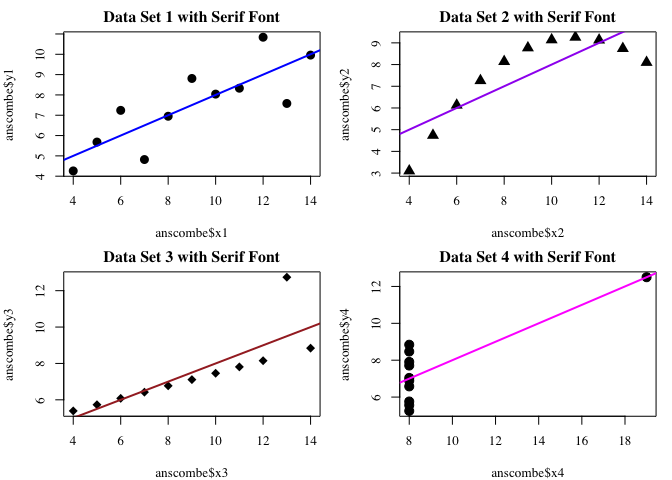
3. Fine-tune the charts without using other packages
- Use a serif font
# Set up graphics parameters to use a serif font
par(family = "serif")
# Recreate plots for each dataset using a serif font
par(mfrow = c(2, 2), mar = c(4, 4, 2, 1))
plot(anscombe$x1, anscombe$y1, pch = 16, cex = 1.5,
main = "Data Set 1 with Serif Font")
abline(lm1, col = "blue", lwd = 2)
plot(anscombe$x2, anscombe$y2, pch = 17, cex = 1.5,
main = "Data Set 2 with Serif Font")
abline(lm2, col = "purple", lwd = 2)
plot(anscombe$x3, anscombe$y3, pch = 18, cex = 1.5,
main = "Data Set 3 with Serif Font")
abline(lm3, col = "brown", lwd = 2)
plot(anscombe$x4, anscombe$y4, pch = 19, cex = 1.5,
main = "Data Set 4 with Serif Font")
abline(lm4, col = "magenta", lwd = 2)
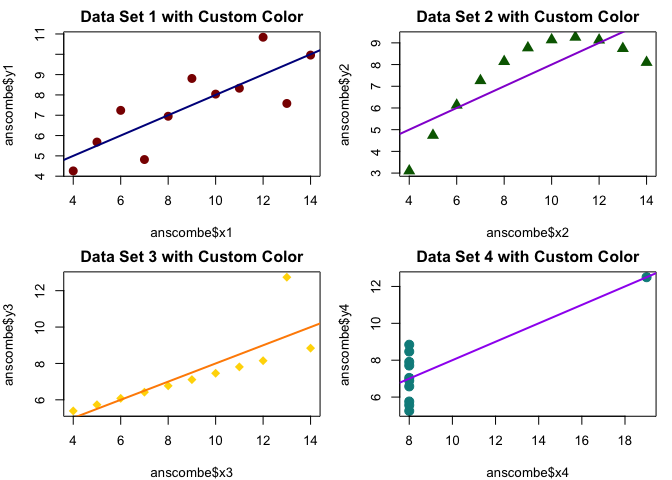
- Use non-default colors
# Use custom colors for the plots
par(mfrow = c(2, 2), mar = c(4, 4, 2, 1))
plot(anscombe$x1, anscombe$y1, col = "darkred", pch = 16, cex = 1.5,
main = "Data Set 1 with Custom Color")
abline(lm1, col = "darkblue", lwd = 2)
plot(anscombe$x2, anscombe$y2, col = "darkgreen", pch = 17, cex = 1.5,
main = "Data Set 2 with Custom Color")
abline(lm2, col = "darkviolet", lwd = 2)
plot(anscombe$x3, anscombe$y3, col = "gold", pch = 18, cex = 1.5,
main = "Data Set 3 with Custom Color")
abline(lm3, col = "darkorange", lwd = 2)
plot(anscombe$x4, anscombe$y4, col = "cyan4", pch = 19, cex = 1.5,
main = "Data Set 4 with Custom Color")
abline(lm4, col = "purple", lwd = 2)
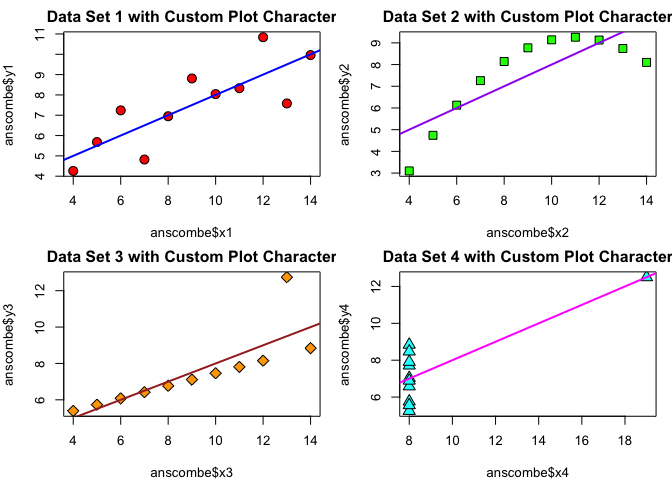
- Use custom plotting character
# Use custom plotting characters
par(mfrow = c(2, 2), mar = c(4, 4, 2, 1))
plot(anscombe$x1, anscombe$y1, pch = 21, bg = "red", cex = 1.5,
main = "Data Set 1 with Custom Plot Character")
abline(lm1, col = "blue", lwd = 2)
plot(anscombe$x2, anscombe$y2, pch = 22, bg = "green", cex = 1.5,
main = "Data Set 2 with Custom Plot Character")
abline(lm2, col = "purple", lwd = 2)
plot(anscombe$x3, anscombe$y3, pch = 23, bg = "orange", cex = 1.5,
main = "Data Set 3 with Custom Plot Character")
abline(lm3, col = "brown", lwd = 2)
plot(anscombe$x4, anscombe$y4, pch = 24, bg = "cyan", cex = 1.5,
main = "Data Set 4 with Custom Plot Character")
abline(lm4, col = "magenta", lwd = 2)
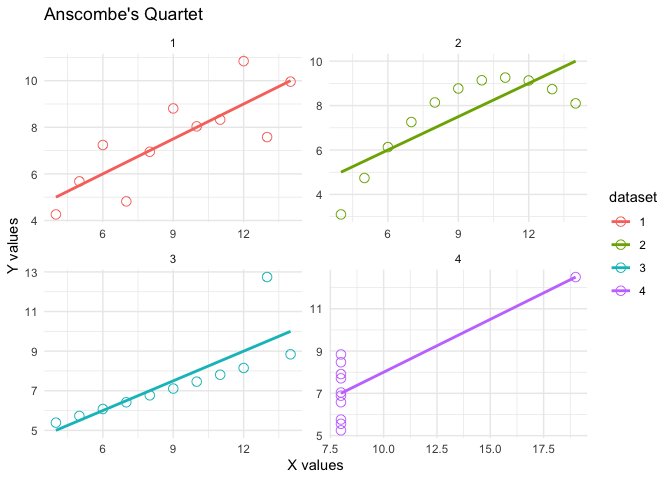
4. Using ggplot2 with the tidyverse package
# Load necessary libraries
library(ggplot2)
# Reshape data for ggplot
library(tidyr)
anscombe_long <- pivot_longer(anscombe, cols = everything(),
names_to = c(".value", "dataset"),
names_pattern = "(.)(.)")
# Create ggplot
ggplot(anscombe_long, aes(x = x, y = y, color = dataset)) +
geom_point(size = 3, shape = 21) +
geom_smooth(method = "lm", se = FALSE) +
facet_wrap(~ dataset, scales = "free") +
theme_minimal() +
labs(title = "Anscombe's Quartet", x = "X values", y = "Y values")
## `geom_smooth()` using formula = 'y ~ x'
Enjoy Reading This Article?
Here are some more articles you might like to read next: